等差数组
413. 等差数列划分
题目描述
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
- 例如,
[1,3,5,7,9]、[7,7,7,7]和[3,-1,-5,-9]都是等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。
示例 1:
输入:nums = [1,2,3,4]
输出:3
解释:nums 中有三个子等差数组:[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。
示例 2:
输入:nums = [1]
输出:0
提示:
1 <= nums.length <= 5000-1000 <= nums[i] <= 1000
方法:差分+计数
如果我们已经求出了 $\textit{nums}[i - 1]$ 以及 $\textit{nums}[i]$ 作为等差数列的最后两项时,答案增加的次数 $t_i$ ,那么能否快速地求出 $t_{i+1}$ 呢?
答案是可以的:
-
如果 $\textit{nums}[i] - \textit{nums}[i + 1] = d$,那么在这一轮遍历中,$j$ 会遍历到与上一轮相同的位置,答案增加的次数相同,并且额外多出了 $\textit{nums}[i-1]$, $\textit{nums}[i]$, $\textit{nums}[i+1]$ 这一个等差数列,因此有: \(t_{i+1} = t_i + 1\)
-
如果 $\textit{nums}[i] - \textit{num}[i + 1] \neq d$,那么 $j$ 从初始值 $i-1$ 开始就会直接退出遍历,答案不会增加,因此有: \(t_{i+1} = 0\)
/**
* 413. 等差数列划分
*
* @param nums
* @return
*/
public int numberOfArithmeticSlices(int[] nums) {
int length = nums.length;
if (length == 1 || length == 2)
return 0;
int sub = nums[0] - nums[1], t = 0, ans = 0; // sub表示数组相邻元素差值
for (int i = 2; i < length; i++) {
if (nums[i - 1] - nums[i] == sub) {
++t; // t可以看作以num[i]结尾的等差数组的数目
} else {
sub = nums[i - 1] - nums[i];
t = 0;
}
ans += t;
}
return ans;
}
446. 等差数列划分 II - 子序列
题目描述
给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。
如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列
- 例如,
[1, 3, 5, 7, 9]、[7, 7, 7, 7]和[3, -1, -5, -9]都是等差序列。 - 再例如,
[1, 1, 2, 5, 7]不是等差序列。
数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
- 例如,
[2,5,10]是[1,2,1,*2*,4,1,*5*,*10*]的一个子序列。
题目数据保证答案是一个 32-bit 整数。
实例1
输入:nums = [2,4,6,8,10]
输出:7
解释:所有的等差子序列为:
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
实例2
示例 2:
输入:nums = [7,7,7,7,7]
输出:16
解释:数组中的任意子序列都是等差子序列。
提示:
1 <= nums.length <= 1000-2^{31} <= nums[i] <= 2^{31} - 1
方法:哈希表+动态规划
- 「以
nums[i]结尾」这件事情肯定要定义在状态中; - 题目不要求连续,因此在求每一个状态的时候,就需要 考虑它之前的所有的元素;
- 能不能接上去,看「公差」,因此记录状态的时候,除了要求以
nums[i]结尾以外,还要记录「公差」,两个整数的差可以有很多很多,因此需要用哈希表记录下来。
到这里为止,每一个 nums[i] 的状态,其实是一张哈希表(键值对),「键」 是 nums[i] 与它前面的每一个元素的「差」,那「值」是什么呢?「值」是以 nums[i] 结尾组成的、公差为某个值的 长度大于等于 2 的等差子序列的个数(就是官方题解中提到的弱等差数列的个数)
状态的「值」是什么?
- 计算「差」,至少需要两个元素;
- 等差数列最开始形成的时候,即:只有两个元素的时候,对结果没有贡献,因为题目要求等差数列的长度至少为 3;
- (这里是重点)如果发现公差相等,才可以找到若干个长度大于等于 3 的等差数列;
- (这里是重点)「弱等差子序列」后面再加上一个数,形成长度更长的等差数列,就是题目中定义的长度大于等于 3 的等差数列,因此在下一次「公差匹配」的时候,记录结果。
以 [2,4,6,8,10] 为例:
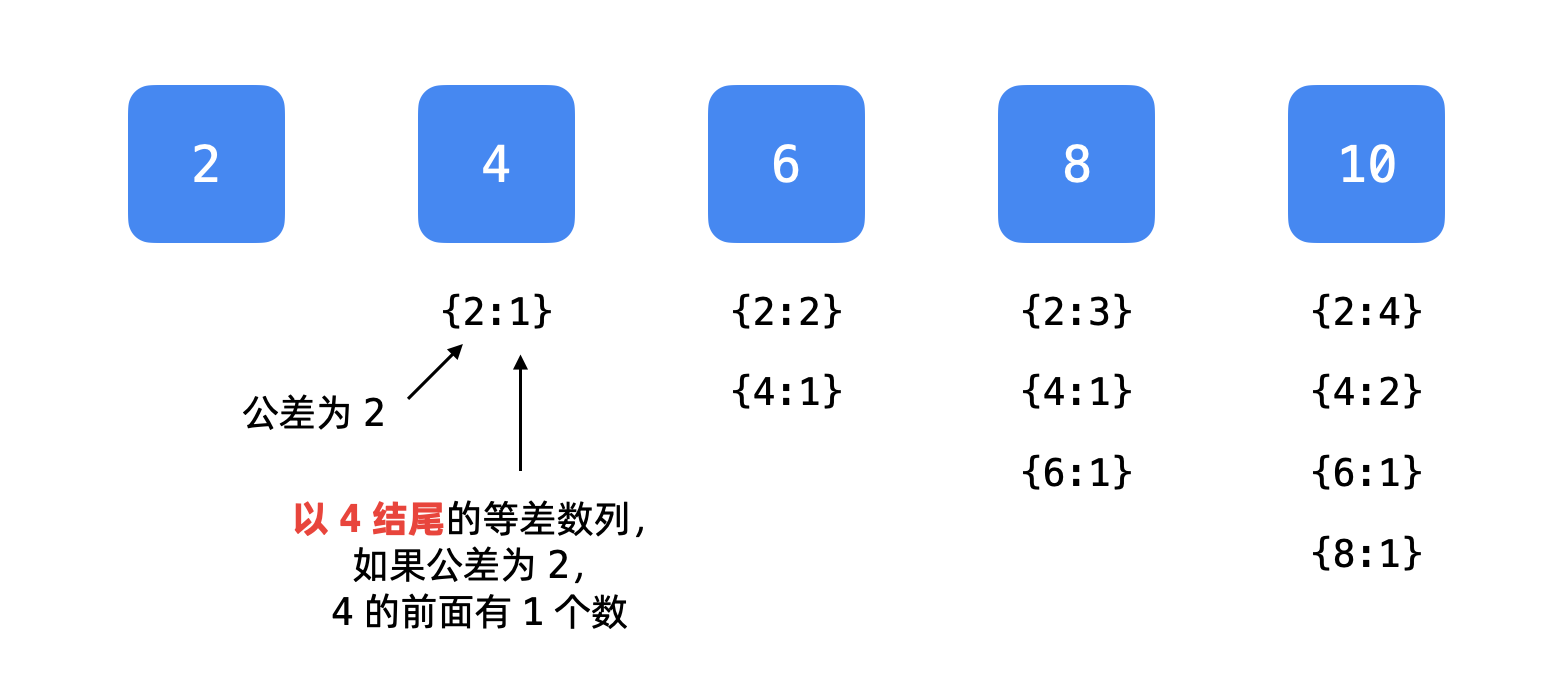
2的前面没有元素,哈希表为空;4的前面只有一个元素2,此时记录键值对{2:1},这里2是「公差」,1是4前面的元素的个数;6的前面有两个元素4和2:6 - 4 = 2,在4的键值对里看一下,有2,说明6可以接在4的后面形成长度更长的等差数列[2, 4, 6],此时记录记录键值对{2:2},同时找到了一个长度为3的等差数列;6 - 2 = 4,在2的键值对里看一下(看第 1 条,哈希表为空),没有4,此时记录{4:1};
8的前面有三个元素6、4和2:8 - 6 = 2,在6的键值对里看一下,有2,说明8可以接在6的后面形成长度更长的等差数列,此时记录键值对{2:3},同时找到了两个长度大于等于 3 的等差数列[4, 6, 8]和[2, 4, 6, 8]8 - 4 = 4,在4的键值对里看一下,没有4,记录{4:1};8 - 2 = 6,在2的键值对里看一下,没有6,记录{6:1};
10的前面有四个元素8、6、4和2:10 - 8 = 2,在8的键值对里看一下,有2,说明10可以接在8的后面形成长度更长的等差数列,此时记录记录键值对{2:4},同时找到了两个长度大于等于 3 的等差数列[6, 8, 10]、[4, 6, 8, 10]和[2, 4, 6, 8, 10](这里的 3 个是基于8的状态值得到的;10 - 6 = 4,在6的键值对里看一下,有4,说明10可以接在6的后面形成长度更长的等差数列,此时记录记录键值对{4:2},同时找到了一个长度大于等于 33 的等差数列[2, 6, 10];10 - 4 = 6,在4的键值对里看一下,没有6,记录{6:1};10 - 2 = 8,在2的键值对里看一下,没有8,记录{8:1}。
class Solution {
public int numberOfArithmeticSlices(int[] nums) {
int length = nums.length;
int ans = 0;
if (length < 3)
return ans;
Map<Long, Integer>[] dp = new HashMap[length];
for (int i = 0; i < length; i++)
dp[i] = new HashMap<>();
for (int i = 1; i < length; i++) {
for (int j = 0; j < i; j++) {
long d = 1L * nums[i] - nums[j];
Integer integer = dp[j].getOrDefault(d, 0);
ans += integer;
dp[i].put(d, dp[i].getOrDefault(d, 0) + integer + 1);
}
}
return ans;
}
}